Dietary macronutrient content, age-specific mortality and lifespan

Abstract

1. Introduction

One of the most well-established ways for extending life is caloric restriction, wherein reducing total calories consumed relative to ad libitum feeding (while avoiding malnutrition) leads to an increase in lifespan [1,2]. More recently, the geometric framework for nutrition (GFN) has provided fresh insights into the effects of diet on lifespan [3,4]. Using diets that differ in calorie density and macronutrient composition GFN studies partition the effects of calorie intake per se from the effects of specific macronutrients in animals with ad libitum access to food. GFN experiments in multiple taxa, including fruit fly (Drosophila melanogaster) and mouse (Mus musculus), show that while holding energy intake constant, decreasing the ratio of protein to carbohydrates (while avoiding malnutrition) extends life [5–7].

These well-established trends pertain to the effects of diet on the population average (often median) lifespan. However, diet can also affect variation in the age at death, even after accounting for effects on the mean [8]. For instance, one meta-analysis found that lifelong diet restrictions (protein and calorie) increase the standard deviation in age at death (s) by 37% on average, and the coefficient of variance (s corrected for the mean) by 48% [9]. Furthermore, a recent GFN study in fruit fly found that the Gini coefficient for age at death (a correlate of s) was increased on high protein, relative high carbohydrate, diets [10].

A demographic parameter that is in many respects more fundamental than either average lifespan, or its variation, is the pattern of age-specific mortality (ASM). Not only do patterns of ASM determine both quantities [11,12], but they provide a higher resolution description of lifespan by partitioning the risk of death across life stages. By representing the whole of life, patterns of ASM describe the sensitivity of different life-history stages to the environment [13], and are therefore useful in thinking about how the optimal environment may change with age. ASM is also a powerful force in life-history evolution. For instance, ecological factors that increase mortality in a specific age class will select for decreased investment in reproductive effort (and the reproductive value) of that age class [14]. Given the link between reproductive value and age, ASMs are considered among the vital rates that determine demography and population growth, making them indispensable to predictive modelling in many fields.

Little is known about how ASM is affected by dietary macronutrient content. Gage & O'Connor [15] tested for associations between ASM and macronutrients in humans using United Nations food-balance sheets. Their results are complex, but generally they find that populations with plentiful access to proteins and fats have reduced mortality across most of life, except infancy; very early life survival was highest where access to carbohydrates was plentiful. Because these analyses are associative, the authors explicitly conclude that ‘causal inferences are not warranted’ [15]. Additionally, their analyses did not correct for socioeconomic factors that improve health (e.g. access to medical care). Many such factors positively correlate with wealth, the overall availability of food and that of fats and proteins. Insights from systems where causality can be inferred (e.g. a GFN experiment) are sparse, with some data coming from invertebrates. For instance, visual comparisons of the mortality kinetics of fruit fly indicate increased ASM at older ages on higher protein diets [16]. In part, robust insights are lacking because methods for concisely modelling ASM have not been incorporated into experimental gerontology, and this is particularly true where data are limited.

Patterns of ASM are summarized in cohort life tables, which represent age as a series of classes. For each class life expectancy at age x (e_x), the probability that an individual at age x will survive, or die prior, to x + 1 (p_x and q_x, respectively; q_x = 1 − p_x), and the proportional cohort survival to x (l_x) is given. Biologists have tended to summarize the patterns in these information-rich life tables as coefficients estimated by fitting an equation to data; the most commonly used are the Gompertz and Weibull equations [17,18]. However, these techniques require large sample sizes (around 100 individuals) to generate meaningful estimates [19]. Fully factorial experiments that segregate the effects of macronutrients and energy are typically restricted in size owing to the number of treatments; GFN studies in vertebrates have 20 or fewer individuals per diet (e.g. [7]).

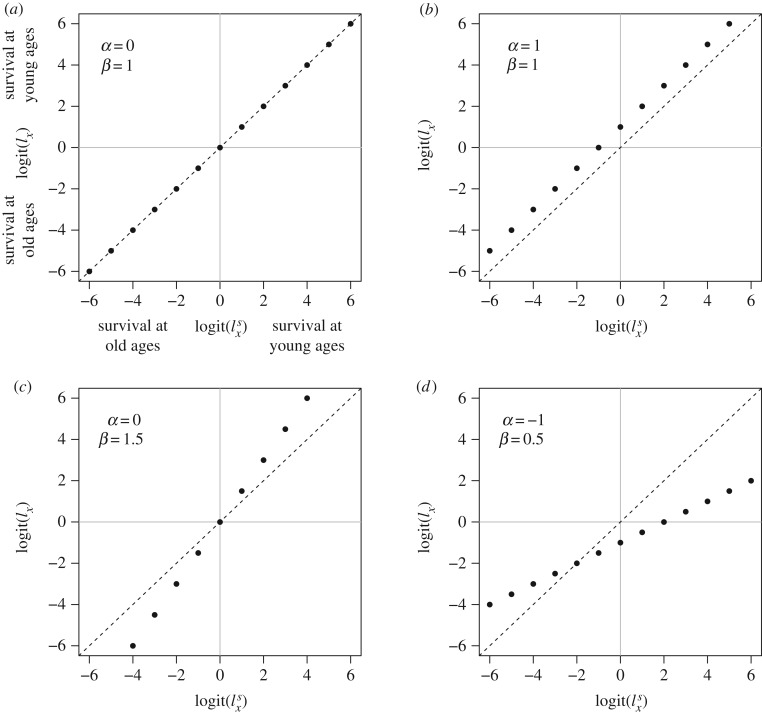
Model life tables are representation theorems used by demographers to model ASM, and have proven particularly useful in populations with limited data because they can leverage more comprehensive datasets [20,21]. A relatively simple technique, which was first systematically explored by William Brass in 1971 [22,23], allows a life table to be condensed to just two parameters. Under the Brass method proportional survival (l_x) for a population of interest can be found following:

where l_x is the survival to age x for a population of interest, lxs is the survival for some comparator pattern that captures the general shape of survival with age (from here on the ‘standard pattern’), and α and β are population-specific constants [22]. Where α is 0 and β is 1 the population of interest has an identical life table to the standard pattern (figure 1a). Values of α less/greater than 0 indicate that overall survival is lower/higher in the population of interest than the standard pattern (figure 1b). Values of β that differ from 1 indicate differences in the decline of survival with age from the standard pattern (figure 1c,d) [23]. For reference, α will tend to correlate with the time-independent coefficient in a two-parameter Gompertz equation, while β will correlate with the time-dependent coefficient, although they should not be interpreted in the same manner. Where a common lxs is used, the estimated α and β from different populations are comparable. From here α and β can then themselves be modelled and life tables constructed. For example, predictive models of α and β based on temporal trends have been used to forecast patterns of ASM [24]. Because of the accuracy of the Brass method, a version slightly modified to account for the specifics of human ASM, is now used by the World Health Organization [20,25].

Open in a separate window

Figure 1.

Effects of α and β on the difference between the predicted logit age-specific probability of surviving to age x (l_x) in a population of interest and a standard pattern (lxs); predictions are given by logit(l_x) = α + β × logit(lxs). Dashed (parity between l_x and lxs) and grey (zero) lines, added for reference.

Here we use the Brass method to explore how ASM is affected by dietary macronutrient content in the mouse. We calculate α and β for 25 diets that vary in their content of protein, carbohydrate, fat and overall energy density. We then model α and β over the macronutrient space captured by the diets. Using predicted values of α and β we calculate life tables, life expectancies and variation in age at death as function of dietary macronutrient content. Finally, we use life table response experiment (LTRE) analysis to determine how patterns of change in life expectancy and variation in age at death are driven by the underlying effects of dietary macronutrient content on ASM [12,13].

2. Method

(b) Analyses

All analyses were performed using R v. 3.5.1 [27]. For each diet, we estimated proportional survival to age x (l_x) based on the observed ages at death using the ‘survfit’ function in the survival package in R. For each diet, we then estimated the parameters α and β using a linear regression equivalent to equation 1 (‘lm’ function), where the response variable was the logit-transformed values of l_x, and the predictor is logit-transformed survival at an equivalent age on the common standard pattern (lxs). Any life table can be used for lxs so long as it captures the general shape of mortality with age and is comprehensive (i.e. survival at a large number of age classes is known). Where there is little justification for which table to use, Brass recommended some average of those that are subject to analysis [22]. We used a life table constructed from all animals in the study irrespective of diet (figure 2a). This means that values of α and β can be thought of as representing deviations in the pattern of ASM of specific diets from the global pattern of ASM from all mice in the study. This method yielded values of α and β for individual diets that give predicted age-specific survivals with good fit to the observed patterns of survival (figure 2b).

Open in a separate window

Figure 2.

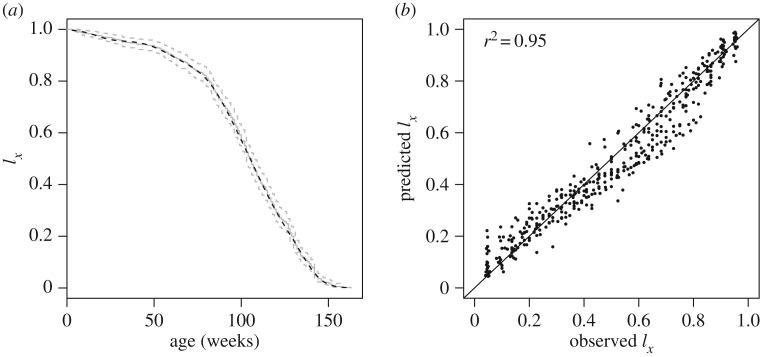
(a) Survival (l_x) by age (weeks) of all animals in the study irrespective of diet. Grey line is a Kaplan–Meier survival curve (dashed lines indicate the upper and lower 95% confidence limits). Black dashed line is the prediction from a GAM where logit survival was fitted as the outcome and age as a smoothed predictor (edf = 8.9, ref.df = 9, F = 5788, p < 0.001). Fitted values (black line) were used as lxs in all analyses. (b) Association between observed values of l_x based on ages at death, and predicted values given by logit(l_x) = α + β × logit(lxs) using diet-specific estimates of α and β (electronic supplementary material, table S1), and lxs (a). r² is based on Pearson correlation coefficient.

To test for effects of dietary composition on α and β, we used generalized additive models (GAMs). A GAM was specified for each of α and β, where the estimated parameter on each diet was fitted as the response, with the macronutrient content of the diet (protein, carbohydrate and fat kJ g⁻¹) fitted as a three-way smoothed predictor. Each response was weighted by the inverse of the sample variance (SE² from the regression) for the outcome on each diet, allowing us to account for imprecision of estimates of α and β (similar to a meta-analytic model; [28,29]). For interpretation, we generated predictions from GAMs for a matrix of representative coordinates within the nutrient space captured by the experiment. These predictions were then visualized as nutrient surfaces showing the effects of dietary macronutrient content on α and β. GAMs were fitted via restricted maximum likelihood using the ‘gam’ function in the mgcv package in R [30].

Interpreting the effects of macronutrients on ASM directly from α and β is challenging. Therefore, GAM-predicted values of α and β were transformed to cohort life tables for ages 3 through 163 weeks (i.e. the beginning of the study through the maximal lifespan observed) giving us a representation of ASM across the nutrient space. For life tables, l_x was calculated via equation (1.1) fixing l₃ at 1 and l₁₆₃₊₁ at 0, and p_x and q_x were calculated following equation S1 (electronic supplementary material, text S1). From here, we calculated life expectancy at age 3 (e₃) and the standard deviation in age at death (s) following eqn 6 and table 2 of van Raalte & Caswell [12], respectively (see equations S2–S4; electronic supplementary material).

Both e₃ and s are ultimately determined by q_x. Analytical expressions (and associated R code) for the sensitivity of e_x and s to q_x based on perturbation analysis are given in the appendix of van Raalte & Caswell [12]. Based on the associated sensitivities, it is possible to use LTRE analysis to decompose changes in e₃ and s as a function of some variable to contributions from the effects of that variable on q_x. For example, van Raalte & Caswell [12] use this method to assess how temporal changes in s and e₀ are driven by concomitant changes in q_x. We use the same approach to decompose changes in e₃ and s as a function of dietary macronutrient ratio to contributions from changes in q_x. (see equations S5 and S6; electronic supplementary material).

3. Results

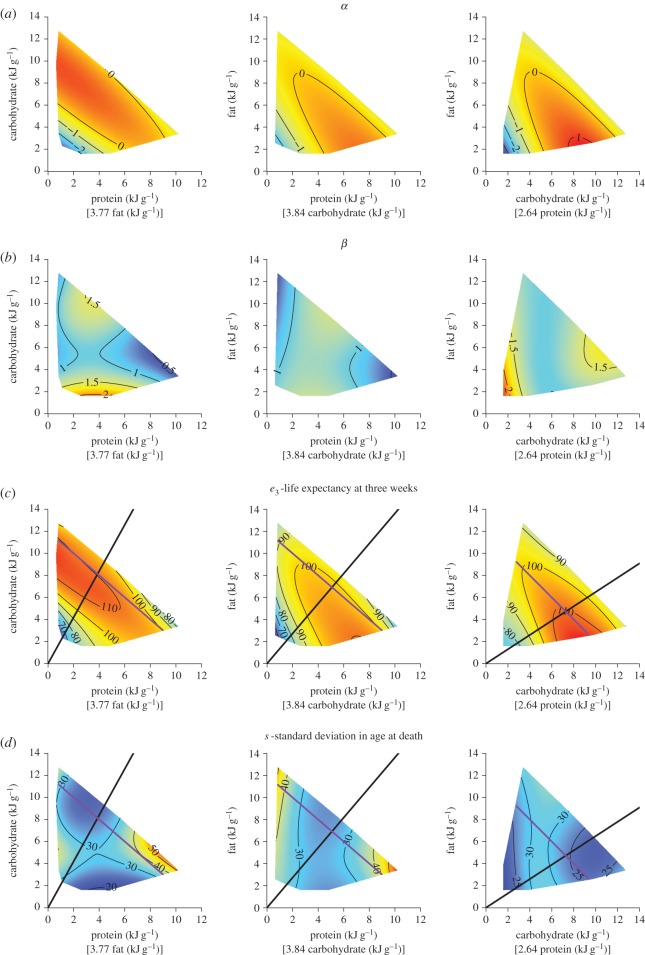
The estimated values of α and β for each of the 25 diets are given in electronic supplementary material, table S1. We detected statistically significant effects of dietary macronutrient content on both parameters (figure 3a,b). α was maximized on diets high in carbohydrate, and low in fat and protein (figure 3a). Diets low in all forms of dietary energy had the lowest values of α. There were complex effects of macronutrients on β. Protein had a nonlinear effect, whereby β was maximized on moderate values of dietary protein (figure 3b). Diets very low in carbohydrate and fat were also predicted to have high β. Figure 3c shows the estimated life expectancy in weeks at the beginning of the experiment (e₃), based on α and β. Here e₃ was highest on diets with low fat content, low to moderate protein and moderate to high carbohydrate. In addition, e₃ was particularly low on diets with low energy density, and also those with very high protein or fat (figure 3c). Diets of intermediate protein content had low standard deviation in age at death (s), while diets very high in protein or fat content generate substantial s (figure 3d).

Open in a separate window

Figure 3.

Surfaces showing GAM predictions for (a) α (GAM three-way smooth term edf = 8.03, Ref. df = 8.06, F = 2.82, p < 0.05, deviance explained = 59%) and (b) β (GAM three-way smooth term edf = 9.94, Ref. df = 10, F = 8.47, p < 0.001, deviance explained = 86%) as function of dietary macronutrient content (kJ/g of food). α and β correspond to coefficients for the equation, logit(l_x) = α + β × logit(lxs), where l_x is the proportion of a cohort surviving to age x on a diet and lxs is the standard pattern of survival (survival of all mice in the study; figure 2a). (c) Life expectancy in weeks at age 3 (e₃; beginning of the study) and (d) standard deviation in age at death (s), based on corresponding values of α and β. From left to right, the panels reflect (i) protein and carbohydrate, (ii) protein and fat and (iii) carbohydrate and fat on the x- and y-axes, respectively (assuming the third nutrient is fixed at the median value shown). Contour values represent the predicted value, and surfaces are shaded such that blue areas reflect low values, while red reflect high values. In (c,d), black lines show an estimate of the ratio of macronutrients consumed by mice under free choice [26,31]. Grey dashed lines indicate isocaloric vectors where the ratio of nutrient x to y changes, but the two collectively constitute 12 kJ g^–1 of the diet. (Online version in colour.)

The self-selected ratio of macronutrients eaten by mouse has been experimentally defined in terms of protein to non-protein energy (around 23% protein; [31]). The self-selected ratio of carbohydrate to fat has yet to be fully characterized. However, Solon-Biet et al. [26] detected asymptotic effects of macronutrient ratio on intake, giving an estimate of the effect of macronutrient ratio on intake. Averaged, the results of the existing studies suggest mice self-select a diet comprising 22% protein, 47% carbohydrate and 31% fat. This estimate of the self-selected diet falls in an area of nutrient space, with relatively high e₃ and very low s (black lines, figure 3c,d). A point of note is that these estimates are based on relatively young animals (less than 15 weeks of age; [26,31]).

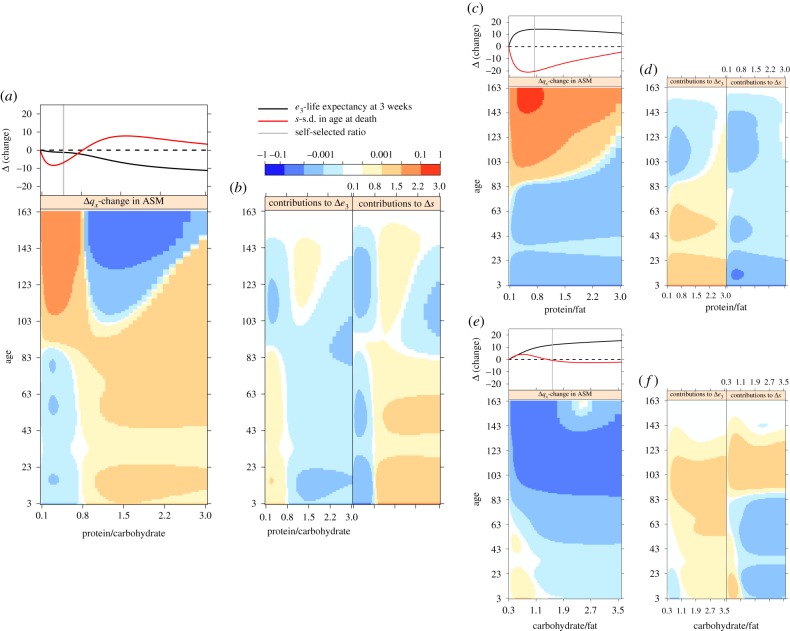
We next identified three isocaloric vectors across the nutrient surfaces (grey dashed lines, figure 3c,d). Figure 4a shows the change in ASM for each age class (q_x), as well as overall e₃ and s, as a function of increasing the protein to carbohydrate ratio (P : C) along the first vector. Increasing P : C initially leads to declines in early life mortality but increases in late-life mortality. As P : C becomes greater than 1, we see reductions in late-life mortality and increases in mortality across early and middle age (figure 4a). At P : C greater than 2.2, we see high q_<130. The contributions of the changes in ASM to overall changes in e₃ and s are also given (figure 4b). Reductions in e₃ at P : C greater than 1.5 are heavily driven by increased mortality below 103 weeks, in particular q_<23, but also q₈₃ to q₁₀₃ (figure 4b). Low levels of s around the self-selected ratio are caused by a combination of low q_<85 and high q_>90.

Open in a separate window

Figure 4.

Change in (a, upper) life expectancy in weeks at age 3 (Δe₃), standard deviation in age at death (Δs) and (a, lower) probability of dying between age x to age x + 1 (Δq_x) as a function of protein to carbohydrate ratio along the isocaloric vector identified across the surfaces in figures ​figures33c,d; protein and carbohydrate collectively contribute 12 kJ g⁻¹, while fat content is 3.77 kJ g⁻¹. Values are relative to that for the minimal nutrient ratio assessed. (b) Heat maps show the proportional contributions of Δq_x to differences in life expectancy e₃ and s as a function of macronutrient ratio. Note colour scales change by a factor of 10. (c,d) As in panels a,b, but as a function of protein to fat ratio along an isocaloric vector, where protein and fat collectively contribute 12 kJ g⁻¹, while carbohydrate content is 3.84 kJ g⁻¹. (e,f) As in panels a,b, but as a function of carbohydrate to fat ratio along an isocaloric vector, where carbohydrate and fat collectively contribute 12 kJ g⁻¹, while protein content is 2.64 kJ g⁻¹. (Online version in colour.)

Increases in the protein to fat ratio (P : F; second isocaloric vector) are initially associated with increasing e₃ and decreasing s, although once the P : F exceeds the self-selected ratio e₃ declines and s increases (figure 4c). Across this vector, the self-selected P : F ratio is associated with maximal e₃ and minimal s (figure 4c). Interestingly, the self-selected P : F ratio is also associated with among the highest levels of late-life mortality. However, any such negative contributions to e₃ are more than offset by heavy positive contributions to e₃ from improved early life survival (figure 4d). The very low levels s on the self-selected P : F ratio is driven by changes in mortality across the board but receives particularly strong negative contributions from improved mortality at q_x<25. Finally, increasing carbohydrate content relative to fat (C : F) is associated with large increases in e₃, and has a nonlinear but relatively minor effect on s (figure 4e). High levels of C : F decrease q_x across all ages increasing e₃, but the strongest positive contributions come from improved survival between 50 and 120 weeks (figure 4f).

4. Discussion

We used model life tables to estimate how dietary macronutrient composition affects patterns of ASM, and in turn, overall life expectancy. Proteins and fats were associated with reduced life expectancy, while carbohydrates tended to be protective. This result concords with alternative analyses of the effects of dietary macronutrient content on median lifespan in this same dataset, and others [5,26]. We also found that a lifelong diet with a macronutrient composition that is self-selected by mice (in early adulthood) was associated with reasonably high life expectancy. Because we were able to estimate the contributions of ASM to life expectancy, we saw that this occurs because the self-selected ratios of P : C and P : F result in low mortality in early and middle age (prior to 85 weeks), but have higher levels of mortality at later ages.

Diets either rich in protein or fat content were associated with a great deal of among-individual variation in the age at death. By contrast, because the self-selected composition has low mortality in early and middle life, but high mortality in later life, this diet minimizes variation. In human populations, variation in age at death has been interpreted as evidence for inequality (i.e. sociological heterogeneity; e.g. [32–34]). However, variation in age at death is not necessarily a signal of variation among individuals and will to some extent be driven by stochasticity. For example, in a homogeneous system where all individuals experience the same age-constant probability of mortality, the standard deviation in the age at death would be equal to the life expectancy, due to stochasticity [12]. Thus, in a controlled experimental system such as ours it is worth considering whether diet affects variation in the age at death via any meaningful effect of diet on variation in biological function.

It seems unlikely that within-diet variation in the age at death is purely stochastic. First, concluding that all individuals on a diet experience identical ASM is analogous to stating that there is no among-individual within-treatment phenotypic variation. This is not the case here; there are substantial differences among individuals in a number of phenotypic measures including food intake, body mass, body composition and circulating concentrations of branched-chain amino acids [26]. Second, these results form part of an emerging pattern, which suggests that diets with macronutrient imbalances are associated with increased phenotypic variability. This pattern includes traits that are less sensitive to non-biological stochasticity in their expression than age at death; traits included are reproductive function, repeatable behavioural traits, traits subject to sexual selection and even human body composition [35–38]. We thus think it credible to conclude that dietary macronutrient content alters biological heterogeneity in a way that affects among-individual variation in age at death.

There is a large literature on extreme, or ‘stressful’, environments as a source of phenotypic variation [39]. The field has tended to focus on the role that the environment plays in releasing hidden genetic variation [40]. Genetic variation does play a role in governing the response to dietary composition, as evidenced by the variable effects seen in different strains of the same species [41–44]. However, in the present study we dealt with individuals of the same strain (cf. [45]). Rather, our analyses imply increased variability in the expression of the same genotype as the environment becomes more nutritionally imbalanced. One possibility is that macronutrient imbalances increase random errors in developmental and regulatory systems, and/or decrease the capacity to buffer against such errors: ‘developmental noise’ and ‘developmental stability’, respectively, or collectively ‘developmental imprecision’ [46,47]. Errors during development that go uncorrected can affect survival, thus generating variation in longevity [46]. Developmental noise (i.e. the rate of errors) is affected by within-individual competition for limiting resources [48]. In great tits (Parus major) for example, diets low in calcium increase the number of errors during feather formation [49]. At the other end of the spectrum, excessive protein could generate an uneven distribution of amino acids within the organism. Diets may also affect the capacity of developmental and regulatory systems to buffer against errors. Integration (i.e. correlated development) is an important source of developmental stability [50], which can be affected by diet. For instance, eating foods that are soft during development reduces the degree of correlation among integrated facial traits in baboons (Papio sp.) leading to increased phenotypic variation [51].

Fixing dietary composition across life as an organism's requirements change has consequences for life history. On the other hand, changing macronutrient content, as a function of age, can maximize important functional traits. For example, our results indicate that it may be possible to minimize ASM across life and maximize life expectancy by altering the ratio of protein to carbohydrate (at a total 12 kJ g⁻¹ with fat constant at an additional 3.77 kJ g⁻¹). Prior to 85 weeks of age, mortality was minimized on a diet comprising around 0.5 parts protein to each part carbohydrate. However, as animals aged beyond 85 weeks, diets with around 1.25 parts protein to carbohydrate were associated with the lowest mortality. These findings mirror epidemiological data from humans and mouse models of cancer, which indicate that prior to old age, diets low in (animal) proteins are protective, but not in older age [52]. A clear experimental question is ‘are there benefits to increasing dietary protein as animals reach middle age? Alternatively, are the late-life benefits of higher protein diets only realized following a lifetime on the diet, which risks death at earlier ages?’ There are two caveats to note here. The first is that our results are inapplicable to infancy (less than three weeks), which is not considered here. The second is that the proposed diet is designed to minimize ASM. However, a diet optimized for reproductive function is likely to be different; higher protein diets tend to improve reproductive parameters in multiple species (e.g. [6,7,53,54]). Because evolutionary fitness is a product of ASM and reproductive function animals may not necessarily have evolved to self-select diets so as to minimize ASM across life.

We have shown that dietary macronutrient content affects life expectancy and variation in the age at death in mice by altering patterns of ASM. We found that the mouse's self-selected diet composition is associated with reasonably long life expectancy and little variation, a pattern produced by low rates of mortality in early and middle age, but high rates in old age. By contrast, diets rich in proteins or fats relative to carbohydrates produce low life expectancy and generate variation by increasing mortality rates across most age classes.

Supplementary Material

Acknowledgements

References